De natuur schijnt merkwaardig genoeg een voorkeur te hebben voor het getal 1. In 1938 publiceerde de natuurkundige Frank Benford een artikel, waarin hij het verschijnsel beschrijft dat in een verzameling getallen de meeste van die getallen met een 1 beginnen. Oorspronkelijk was dit idee in de 19e eeuw al naar voren gebracht door de sterrenkundige Simon Newcomb. Benford toonde aan dat de kans dat in een reeks getallen een getal met een D begint gelijk is aan log10(1 + 1/D). De kans dat het een 1 is bedraagt 30,1%, een 2 17,6% en een 3 is 12,5%. Onlangs heeft een drietal wetenschappers onder leiding van seismoloog Malcolm Sambridge uit Australië 15 verzamelingen bekeken van data uit diverse wetenschapsdisciplines en daaruit kwam naar voren dat de wet van Benford daadwerkelijk geldt in de natuur. In de sterrenkunde keken ze bijvoorbeeld naar gegevens van de hoeveelheid fotonen die verre gammabronnen uitstralen, zoals waargenomen door de Fermi satelliet (zie afbeelding – photon fluxes of bright objects), en naar de rotatiesnelheid van pulsars. Andere datsets betroffen bijvoorbeeld de hoeveelheid door ziektes getroffen mensen en de diepte van de epicentra van aardbevingen. Allen bleken ruwweg de wet van Benfordte volgen. Opmerkelijk was dat in het geval van de aardbevingen uit de gegevens een zeer kleine aardbeving tevoorschijn kwam die moest hebben plaatsgevonden in Australië ten tijde van de grote tsunami die december 2004 plaatsvond. Die was op dat moment kennelijk niemand opgevallen, maar hij was wel degelijk gebeurd. Bron: New Scientist.
Astronomisch nieuws, wetenswaardigheden én persoonlijke opinies
Recente berichten
- Team geografen brengt UFO hotspots in de VS in kaart; het Westen ‘ziet’ de meeste UFO’s
- Venus blijkt zuurstof en koolstof te ‘lekken’ uit zijn magnetosfeer
- Ten dode opgeschreven komeet gefotografeerd tijdens de totale zonsverduistering
- Dopplerverschuiving van radiosignalen gemeten tijdens de laatste zonsverduistering in de VS
- Hubble constante bepaalt met behulp van supernova H0pe
Archief Astroblogs per maand
Meest gebruikte Astroblogs tags
67P
ALMA
astrofotografie
Cassini
Chandra
clusters
Curiosity
donkere materie
ESA
ESO
exoplaneten
Higgs bosonen
Hubble
infografieken
ISS
Jupiter
JWST
Kepler
kometen
LHC
maan
Mars
Melkweg
Mercurius
NASA
New Horizons
planetoïden
Pluto
pulsars
Rosetta
Saturnus
Sojoez
SpaceX
sterrenstelsels
stervorming
supernovae
superzware zwarte gaten
Venus
VLT
water
Webb
witte dwergen
zon
zwaartekrachtgolven
zwarte gaten
Copyright © 2024 · Genesis Framework · WordPress · Log in
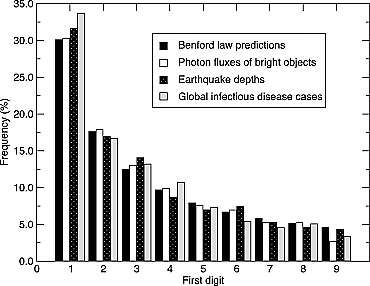




Dit is misschien wel 1 van de meest bizarre dingen die ik de laatste tijd gelezen heb. Het is fascinerend dat de natuur schijnbaar een voorkeursgetal heeft…..ik vraag me af wat voor proces hiervoor verantwoordelijk kan zijn. Je kan echt je hoofd breken over dit soort dingen. Heeft iemand een suggestie?
@Olaf van Kooten,
Beste Olav,
Het is niet zo moeilijk om dat te begrijpen. De wet van Benford geldt voor getallen die op meetbare grootheden slaan, niet op zomaar verzonnen getallen.(Je kunt immers altijd getallen verzinnen die er niet aan voldoen). En meetbare grootheden worden altijd in een bepaalde EENHEID uitgredrukt, b.v. in meters of in kilo's of in euro's. Als je nu b.v. de eenheid halveert dan verdubbelen alle getalswaarden. In de nieuwe maat zijn alle getallen dus twee maal zo groot. Alle getallen die met een 1 begonnen, de 1-getallen, beginnen nu met een 2 of een 3 en worden dus 2-getallen of 3-getallen. En alle 5-, 6-, 7-, 8- of 9- getallen worden 1-getallen. Toch moeten die getallen weer dezelfde verdeling opleveren. Er moetenn dus even veel 1-getallen in de verdeling gezeten hebben dan er 5-, 6-, 7-, 8- of 9- getallen waren. Die getallen zelf beslaan resp. de trajecten tussen 1 en 2 en die tussen 5 en 10. En dat geldt natuurlijk voor iedere schaalverandering van de betreffende grootheid. En dit kan alleen wanneer de dichtheid van de getallen OMGEKEERD evenredig is met de getalwaarden zelf. Er zijn er dus veel meer die met een 1 beginnen dan die er met een 2, 3, … of 9 beginnen.
Als je verder geïnteresseerd bent kun je me mailen en stuur ik je er een artikieltje over op.
Gerrit Bosch
Misschien is een verklaring gelegen in de wijze waarop wij dingen meten. De flux fotonen bijvoorbeeld die afkomstig is van gammaflitsers meten we in bepaalde eenheden, bijv. x joules/sec. Bij die eenheden kunnen de gemeten waarden dan in 30% van de gevallen met een 1 beginnen. Zou die eenheid van joule zelf een andere waarde hebben, dan zou de uitkomst zijn dat bijvoorbeeld 30% met een 6 begint. Kortom, het begint met de eenheden waarin je de verschillende soorten van data uitdrukt en die eenheden zijn door mensen gedefinieerd.
De natuur heeft een voorkeur voor het "decimale cijfer 1 aan het begin van getallen".
En voor elke decimaal kun je een 0 zetten.