Gisteren had Olaf van Kooten hier het verhaal van de tweede satelliet van de Aarde, de kleine planetoïde 3753 Cruithne. Maar naast onze echte maan en deze kleine, vijf kilometer grote steenklomp, is er nóg een object dat als een soort van begeleider van de aarde kan worden beschouwd. In oktober 2010 werd namelijk met NASA’s Wide-field Infrared Survey Explorer (WISE) missie 2010 TK7 ontdekt, een 300 meter grote planetoïde, die in baan met de vorm van een zadel om Lagrangepunt L4 van de aarde draait. Je ziet hierboven 2010 TK7, op de door WISE gemaakte foto, dat puntje in de groene cirkel. Het punt L4 bevindt op de baan van de aarde, met een ‘voorsprong’ op de aarde van 1 maal de afstand aarde-zon (in rechte lijn, niet langs de kromming van de baan). Hieronder zie je alle Lagrangepunten van de zon en aarde, L1 tot en met L5.
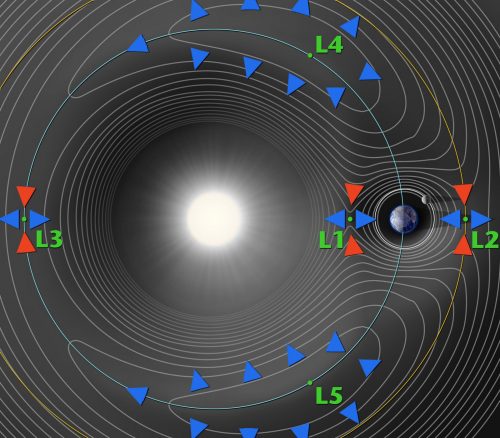
De Lagrangepunten. Credit: Neil J. Cornish / NASA / WMAP science team, via http://map.gsfc.nasa.gov/mission/observatory_l2.html.
Planetoïden die zich bevinden in de Lagrangepunten L4 en L5 van een planeet worden Trojanen genoemd. Mars heeft Trojanen in L4 en L5, Jupiter heeft ze, Saturnus heeft ze, Neptunus heeft ze en zelfs twee manen van Saturnus zijn in het bezit van Trojanen. Lange tijd was de vraag of de aarde ook zo’n Trojaan heeft en toen ik augustus 2010 over deze vraag blogde was het antwoord ‘dat weten we niet’. Maar zoals gezegd, twee maanden na mijn blog ontdekte men 2010 TK7 met de infrarood-satelliet WISE en dat bleek een echte aardse trojaan te zijn, de enige die tot nu toe bekend is. Hieronder zie je z’n baan in 2011, waarin je ziet hoe 2010 TK7 in een soort zadelvorm om L4 draait.
Dat 2020 TK7 daarbij niet in het eclipticavlak blijft, het vlak van de aarde in haar baan om de zon, blijkt wel uit de afbeelding hieronder, waarin je de baan van de trojaan driedimensionaal ziet. Iedere ‘loop’ van de groene cirkel stelt de baan van 2010 TK7 in één jaar voor, de blauw stippen stellen de baan van de aarde om de zon voor.
Bron: Starts with a Bang.

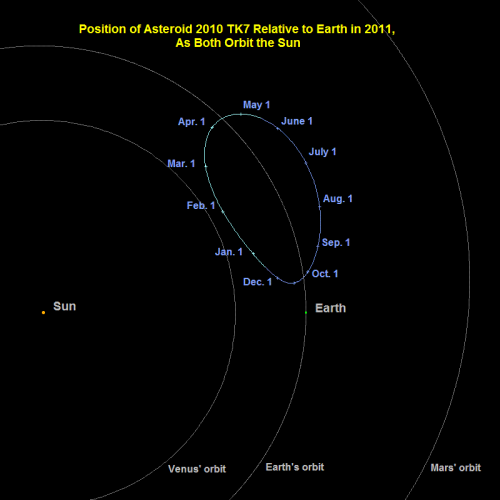
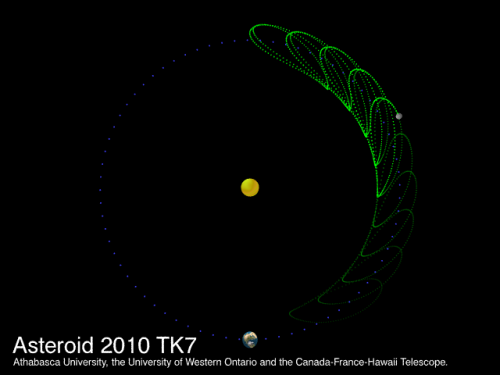





Nou Arie…die baan van 2010 TK7 kan ik helemaal niks van bakken. Denk niet dat ik eruit kom met een beetje Newton 🙂
Althans als ik de groene cirkel in dat plaatje goed begrijp…
Hier een animatie waarin je de baan van 2010 TK7 ziet. Wellicht dat dat verheldering geeft.
http://youtu.be/VGmdSbtkFS0
Dank! Dat is een stuk duidelijker. Maar ik kan nog niet die baan verklaren 🙂
Het is in orbit om “niets” en het lijkt wel of het op een golf van zwaartekracht surft. Maar ja zwaartekracht kan niet duwen. Het doet me denken aan dat warpspeed gebeuren van star trek 🙂
Weer iets om een weekend mee door te komen. Gelukkig is het vrijdag
Edit
Ow, tis vanuit de Aarde gezien, net zoals we Mars af en toe in de achteruit zien schakelen?
Het punt is nou juist dat een Lagrange punt niet niets is. 😉
groet,
Gert (Enceladus)
Ok, maar het is toch een soort van centrum van zwaartekrachtvelden veroorzaakt door 2 (of meer?) massieve objecten? Dus zeg maar een plek waar, in dit voorbeeld, de Aarde even hard aan 2020 TK7 trekt als de Zon? Misschien begrijp ik zo’n locatie verkeerd, maar als het klopt wat ik zeg, kan ik nog steeds niet die baan van 2020 TK7 verklaren…. 🙁
Ja, dat klopt. En voor zover ik het begrijp draait 2010 TK7 daar dan kleine baantjes om heen. Dat wil zeggen: ik kan me niet goed voorstellen dat het een grote omloopbaan zal zijn. Kan iemand iets zeggen over de grootte van die omloopbaan?
groet,
Gert (Enceladus)
Correctie op mijzelf: als ik de illustraties hierboven bekijk, dan lijkt het toch een flinke baan te zijn!
groet,
Gert (Enceladus)
Na de post over Cruthne was het wachten natuurlijk op een artikel over 2010 TK7. Astroblogs stelt me wederom niet teleur!
Waar ik me over verbaas is dat 2010 TK7 niet om L4 (60° vòòr de Aarde, in de baan van de Aarde) lijkt te draaien. *Lijkt*, want Chodas en Yeomans hebben in 2011 de baan tot ca. 2209 berekend:
http://neo.jpl.nasa.gov/news/news173.html
Niet logisch , deze Trojaan waar draait deze omheen dan ???
of het filmpje is fout in animatie ,
gaan we naar 1 april ? we zullen het tegen die tijd wel weten haha
Waarom niet logisch? Hij draait wel degelijk ergens omheen en wel om Lagrangepunt L4. In de Astroblog staat een link naar een andere blog waarin ik die Lagrangepunten uitleg. Nee, de animatie is correct. En nee, het is geen 1 april grap. Zou een beetje vroeg daarvoor zijn.
Zoals de vraag gesteld wordt kun je niet zeggen dat 2010 TK7 om het Langrangepunt draait. 2010 TK7 draait om de Zon! En omdat hij dat in bijna dezelfde baan als de Aarde doet wordt die baan beïnvloed. Die verstoring zorgt er voor dat de Trojaan rond het Langrangepunt L4 blijft wiebelen. Dat Langragepunt draait met de Aarde mee ook om de Zon.
Paul, bedankt voor je aanvulling. Het is een mix van bewegingen die 2010 TK7 maakt. Zoals de aarde en de maan om een gemeenschappelijk zwaartepunt draaien (een punt dat geloof ik ergens onder het aardoppervlak is gelegen), zo draaien aarde en maan samen weer om de zon. En zo draait 2010 TK7 ook om de zon en om dat punt L4, dat door de gezamenlijke zwaartekracht van zon en aarde wordt gevormd.
Ja. En lagrangepunten L4 en L5 zijn intuitief moeilijk te bevatten. Ze zijn dan ook (wiskundig) later ontdekt dan L1, L2 en L3. Voor wie het echt wil begrijpen, kijk hier maar eens in:
http://www.math.cornell.edu/~templier/junior/final_paper/Thomas_Greenspan-Stability_of_Lagrange_points.pdf
Dat maakt duidelijk dat het allemaal niet zo eenvoudig is.
Overigens zijn baanresonanties rond L4 en L5 stabieler dan baanresonaties rond L1, L2 en L3.
Dank voor die pdf want met wiki ben ik nog niet veel wijzer geworden.
Voor mij zijn de punten 2 en 3 nog spannender. Ik begrijp dat een object op b.v. L2 dan achter de Aarde zou staan t.o.v. de Zon, en tijdens de omloop om de Zon ook constant achter de Aarde blijft staan. Het object op L2 staat verder van de Zon, maar zijn omlooptijd is even lang als die van de Aarde. De lengte van de omloop is dus langer, dus moet het sneller bewegen om de Aarde bij te kunnen houden. En dat botst gevoelsmatig wel met Newton…..een grotere omloop geeft altijd een langzamere snelheid anders vliegt het uit de bocht. Tenzij dat beetje extra massa van de Aarde samen met de Zon, genoeg is om die grotere baan met hogere snelheid te verklaren.
De massa van de Aarde zorgt er inderdaad voor dat de omlooptijd van objecten net buiten de Aardbaan wordt verkort. En in punt L2 is die verkorting dusdanig dat de omlooptijd van een object in punt L2 rond de Zon gelijk is aan de omlooptijd van de Aarde. Allemaal te berekenen met de wetten van Newton.
De massa van de Aarde doet er dus zeker toe!
Ik vond nog deze animatie met Langrangepunten in het Aarde-Maan systeem:
https://www.youtube.com/watch?v=z52WWLE8bBo
Naar analogie: hier doet de massa van de Maan er zeker toe!
Mooie animatie Paul, maar zoals je zegt geeft dit de Lagragepunten van het Aarde-Maan-systeem weer. En die Lagrange punten draaien uiteraard om onze planeet mee, met de beweging van de Maan.
Het Lagrangepunt waar 2010 TK7 omheen draait heeft hier echter niets mee te maken. Je zou kunnen zeggen dat dat punt zich op dit moment ongeveer bevindt op de plek waar wij op 1 mei zullen zijn.
groet,
Gert (Enceladus)
Ja, Gert, dat klopt. Die animatie was meer voor de uitleg mbt Lagrangepunten in het algemeen en ik zag geen zelfde animatie voor het Zon-Aarde systeem.
Dat had ik wel wat duidelijker kunnen vermelden, in een aparte reactie.
Hoi Paul,
Het was geen kritiek hoor. Maar ik was even op het verkeerde been gezet. Pas in tweede instantie zag ik dat je wel vermeld had dat de animatie de Lagrangepunten van het Aarde-Maan-systeem betreft.
Trouwens, wel een aantrekkelijk idee dat bij L4 eigenlijk al lente is! 😉
groet,
Gert (Enceladus)
Ik denk dat het door mij komt…..ik schreef een stukje over het L2 punt en Paul gaf een reply, volgens mij op mijn geleuter gericht 🙂
Ps Gert, ik hoorde op journaal, en las vervolgens op internet “De meteorologische lente begint op 1 maart en duurt tot en met 31 mei. De astronomische lente begint in de komende decennia vrijwel ieder jaar op 20 maart.”
Nou…..1 maart vandaag…kan m’n winterdepressie de kast weer in, denk je?
Ja, berg ‘m maar gauw op! 😉
groet,
Gert (Enceladus)