Astronomen die gebruik maken van het MUSE-instrument van ESO’s Very Large Telescope in Chili en de Hubble-ruimtetelescoop van NASA en ESA hebben de meest precieze test tot nu toe gedaan van Einsteins algemene relativiteitstheorie buiten de Melkweg. Het nabije sterrenstelsel ESO 325-G004 fungeert als een sterke zwaartekrachtlens en vervormt het licht van een verder weg staand sterrenstelsel tot een Einsteinring. Door de massa van ESO 325-G004 te vergelijken met de kromming van de omliggende ruimte, ontdekten de astronomen dat de zwaartekracht zich op deze astronomische lengteschalen gedraagt zoals voorspeld door de algemene relativiteitstheorie. Daarmee zijn enkele alternatieve zwaartekrachttheorieën ontkracht.
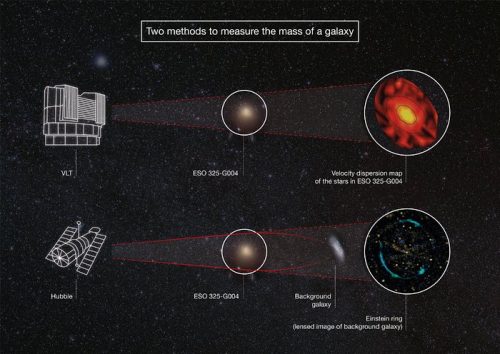
Met behulp van het MUSE-instrument van ESO’s VLT heeft een team onder leiding van Thomas Collett van de Universiteit van Portsmouth (VK) eerst de massa van ESO 325-G004 berekend door de bewegingen van sterren in dit relatief nabije elliptische sterrenstelsel te meten.
Collett legt uit: ‘We hebben gegevens van de Very Large Telescope in Chili gebruikt om te meten hoe snel de sterren in ESO 325-G004 bewegen. Hieruit konden we afleiden hoeveel massa er in dit sterrenstelsel aanwezig moet zijn om deze sterren in hun omloopbanen te houden.’
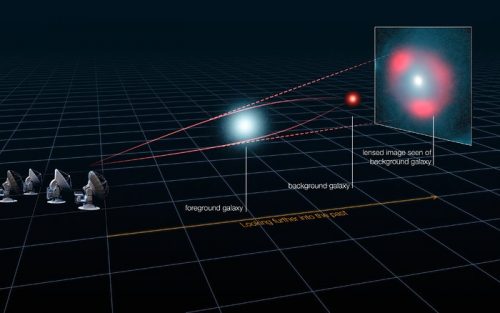
Maar het team heeft ook een ander aspect van de zwaartekracht gemeten. Met behulp van de Hubble-ruimtetelescoop van NASA en ESA namen ze een Einsteinring waar die is ontstaan doordat ESO 325-G004 het licht van een ver verwijderd sterrenstelsel vervormt. Aan de hand van deze waarnemingen konden de astronomen meten hoe licht, en daarmee dus ook de ruimtetijd, door de enorme massa van ESO 325-G004 wordt afgebogen.
Het gravitatielenseffect op verre sterren-vormende sterrenstelsels (schematisch). Credit: ALMA (ESO/NRAO/NAOJ), L. Calçada (ESO), Y. Hezaveh et al.
Einsteins algemene relativiteitstheorie voorspelt dat objecten de hen omringende ruimtetijd vervormen, waardoor passerend licht wordt afgebogen. Dit resulteert in een verschijnsel dat het zwaartekrachtlenseffect wordt genoemd. Dit effect valt alleen op bij objecten die heel veel massa hebben. Inmiddels zijn een paar honderd van die sterke zwaartekrachtlenzen bekend, maar de meeste zijn te ver weg om hun massa exact te kunnen meten. Met een afstand van ‘slechts’ 450 miljoen lichtjaar is het sterrenstelsel ESO 325-G004 een van de meest nabije lenzen.
Collett vervolgt: ‘We kennen de massa van het voorgrondstelsel van MUSE en we hebben de sterkte van het lenseffect gemeten zoals Hubble dat laat zien. Vervolgens hebben we deze twee manieren om de sterkte van de zwaartekracht te meten met elkaar vergeleken, en het resultaat was precies wat de algemene relativiteitstheorie voorspelt, met een onzekerheid van slechts 9 procent. Daarmee is dit de meest precieze test van de algemene relativiteitstheorie buiten de Melkweg tot nu toe. En dit met behulp van slechts één sterrenstelsel!’

Cluster Abell S0740. Credit:NASA, ESA, and The Hubble Heritage Team (STScI/AURA)
Op de schaal van ons zonnestelsel is de algemene relativiteitstheorie met grote nauwkeurigheid getoetst, maar aan nauwkeurige tests op grotere astronomische schalen ontbrak het tot nu toe. Het testen van de langeafstandseigenschappen van de zwaartekracht is van cruciaal belang om de geldigheid van ons huidige kosmologische model te onderzoeken.
Deze bevindingen kunnen belangrijke gevolgen hebben voor alternatieve zwaartekrachtmodellen. Deze alternatieve theorieën voorspellen dat de effecten van de zwaartekracht op de kromming van ruimtetijd ‘schaalafhankelijk’ zijn. Dit betekent dat de zwaartekracht zich op extragalactische lengteschalen anders zou moeten gedragen dan op de kleinere schaal van het zonnestelsel. Collett en zijn team hebben vastgesteld dat dit waarschijnlijk niet het geval is tenzij de verschillen alleen optreden op lengteschalen van meer dan 6000 lichtjaar.
‘Het is geweldig dat het heelal ons lenzen levert die we als laboratoria kunnen gebruiken’, voegt teamlid Bob Nichol van de Universiteit van Portsmouth daaraan toe. ‘Het is zo bevredigend om de beste telescopen ter wereld in te zetten om Einstein op de proef te stellen, en erachter te komen dat hij gelijk had.’ Hier het vakartikel over de test, dat in het tijdschrift Science verschijnt. Bron: ESO.






Grappig dat ene Soldner die Einstein weer voor was…
Christina Turner “The Early History of Gravitational Lensing” Tuesday, February 14, 2006.
“Unaware of Soldner’s earlier work, Einstein obtained the same value for the deflection angle from the principle of equivalence and the assumption that the spatial metric is Euclidean, unaffected by gravity. As the theory of general relativity was not fully developed at this time, Einstein, using the framework of special relativity, obtained the same value as Soldner had calculated using Newtonian physics.”
Of ene Chwolson… http://adsabs.harvard.edu/abs/1924AN….221..329C
His most noted accomplishment was in 1924, when he published about gravitational lenses in Astronomische Nachrichten, a scientific journal on astronomy. The concept of gravitational lenses, did not get much attention until 1936, when Albert Einstein wrote about the gravitational lens effect.[2] The observation of a gravitational lens, where one source (sun or galaxy) produces a ring around another source is referred to as an Chwolson ring, or Einstein ring.
Beetje misleidend artikel. Het is zeker niet de meest precieze tést van GR. Het is de meest precieze méting binnen een smal gebied.
Ik vraag me af wat de uitkomst van een heel precieze meting van de rotatiesnelheid van de buitenste regionen van galaxy clusters zou opleveren. Daar zullen de resultaten (hoewel niemand écht weet wat er aan de hand is) een ander plaatje laten zien.
Begrijp me niet verkeerd; ik ben een enorme fan van Albert. Maar we zien nog niet alles.
Ik zie de misleiding niet hoor. Er staat niet dat het de meest precieze test van de GR is, wel dat het de meest precieze test van de GR buiten de Melkweg is. Als jij een andere test van de GR buiten de Melkweg weet die preciezer is dan deze, dán is het inderdaad een misleidende tekst. Ik hou mij aanbevolen voor een linkje. 🙂
Er bestaat overigens wel een betere test van de GR, gedaan in 2003 met de Cassini ruimtesonde. Maar ja, die keek naar radiosignalen vanaf de aarde die langs de zon scheerden… bínnen de Melkweg. Zie https://www.nature.com/articles/nature01997
Met het begrip “test” bedoel ik het vaststellen van de juistheid, en volledigheid van GR. Men heeft met de bovengenoemde test enkel het zwaartekracht lensing effect buiten het melkwegstelsel gemeten.
Ik schat je dusdanig kundig in, dat je op de hoogte bent van de problemen die GR heeft met het verklaren van de rotatie snelheid van de buitenste regionen van galaxy clusters.
En hoewel ik het prachtig vind, dat men nog stéeds geen speld tussen deze oude theorie heeft kunnen krijgen, beginnen er andere geluiden te klinken. Van mensen die (in tegenstelling tot mijzelf) er wél verstand van hebben.
In de dualiteit tussen GR, en QM verwachten wetenschappers dat GR uiteindelijk het veld zal ruimen.
Ik hoop dat ik het niet mee hoef te maken.
Mies, ik denk dat men onderscheid moet maken
1)tussen lichtfotonen en materie met massa
2) bewegen door een referentierooster en in een referentierooster en er deel van uitmaken
Licht heeft geen massa en dus geen p=mv , een relativistische snelheid en het beweegt zich in het ruimtetijdnet doorheen de krommingen van de massasystemen, waar het het lensingeffect bekomt.
De rotatiesnelheden in de buitenste regionen van een sterrenstelsel gaat over massa’s of sterren die zich met een bepaald p=mv in het gekromde referentierooster van dat sterrenstelsel bewegen en er deel van uitmaken. Zij volgen dus de concentrische geodetische lijnen in evenwicht met MG/R (potentiële energie) van het sterrenstelsel en hun eigen momentum p=mv met kinetische energie mv2/2 dat gelijk is aan 1/2MG/R.
De kromming in die regionen is minder groot per tijd en ruimte zodat uw ruimte daar een paar maal groter is per tijdseenheid van het ruimtetijdnet dan de ruimte per tijdseenheid dichter bij het centrum. Hierdoor is de afstand per tijdseenheid groter zonder de potentiële/kinetische balans te verstoren.
Dit zijn afleidingen uit mijn theorie en ik weet niet in hoever dat de GR benaderd of afbreekt.
Ik hoop je hiermee geholpen te hebben
Groet Marc:)
Volgens mij zit de kloe van het verhaal hem hierin:
Voorheen werden lenseffecten waargenomen en kon men alleen de massa van de lensveroorzaker bepalen met GR/SR a.d.h.v. de buiging van het licht. Maar dan ga je op voorhand uit van een kloppende GR/SR
Nu heeft men niet alleen de massa bepaald a.d.h.v. de lenseffecten, maar ook met behulp van andere waarnemingen aan de lensveroorzaker (het object op de voorgrond), zoals luminositeit en rotatiesnelheden. Zeg maar, meer Newtonian methoden en dat is niet makkelijk bij vergelegen objecten. Uit beiden komt ongeveel dezelfde waarde voor de massa, dus Einstein rijmt met Newton. Dan heb je wel een test waaruit blijkt dat GR/SR moet kloppen
Althans, zo lees ik het geheel.
ps ik weet dat je het schrijft als clou 🙂
Uitstekend verhaal K.J. Dank hiervoor.
Ik zit stilletjes te hopen dat er morgen een verhaal komt van Susskind/Maldacena dat er geen Event Horizons, en zwarte gaten bestaan, en dat Appies werk tot in het einde der tijden een robuuste pilaar in de wetenschap blijkt te zijn.
GR Forever !!!!
Wat ik wel vreemd vind aan die ringen is dat je eigenlijk een regenboog verwacht met rood aan de buitenzijde en blauw aan de binnenkant met hier en daar nog een spectraallijn, immers hoogenergetische fotonen (blauwe) hebben meer equivalente rustmassa en buigen meer af dan de rode fotonen. Zoals al aangegeven in mijn eerste post had Soldner aan de Newton wetten al voldoende om het effect te verklaren.
Omdat dat ook niet gebeurt. Alle golflengtes volgen hetzelfde pad van gebogen ruimtetijd. Ik kan er een lang verhaal over schrijven, maar denk b.v. eens aan waarom een zwaar object net zo snel valt als een minder zwaar object. Of waarom een sateliet van 50 gram dezelfde orbit om de aarde kan volgen als een van 50 kilo. Heeft iets energie (een foton…een baksteen…etc), zal het gebogen ruimtetijd volgen, onafhankelijk van de hoeveelheid energie. Wat wel van invloed is, is de snelheid…..als licht van verschillende golflengtes met verschillende snelheden zou reizen, dan zou je die regenboog moeten krijgen. Maar licht kent maar 1 snelheid (in empty space bedoel ik uiteraard).
Het gaat pas anders lopen als beiden betrokken objecten zoveel massa/energie hebben dat ze beiden ruimtetijd sterk buigen, zoals b.v. twee neutronensterren of zwarte gaten in elkaars orbit
Je gaat me toch niet vertellen dat de gravitatiewet van Newton hier toch niet geldt en Soldner het fout had?
https://nl.wikipedia.org/wiki/Gravitatiewet_van_Newton
F = Gx (m1xm2)/r*2, vul voor het foton de equivalente rustmassa in M1 en voor M2 de gravitatiebron en voila.
Bij iedere golflengte behoort een energie (E=hxf) zodat de rustmassa dus frequentie afhankelijk is.
En F bepaald weer hoeveel een foton met een bepaalde energie door M2 wordt afgebogen.
Of zie ik het nu verkeert?
Wel en niet 🙂
Dat komt omdat hier m1 (sterrenstelsel) een oneindig grote waarde heeft en m2 (foton) een oneindig kleine. Gebruik je de formule voor een roodlicht foton, en vervolgens voor een blauwlicht foton, komt daar afgerond hetzelfde uit. Dus geen regenboog. Misschien als je de roodlichtfoton vervangt voor de maan, en de blauwlichtfoton voor een ster 100 x de massa van de zon, kom je misschien op een noemenswaardig verschil. Newton (zwaartekracht is aantrekkende kracht) is bij benadering ok. Einstein (geen kracht maar buiging van ruimtetijd, en met name van tijd) voor het echte werk.
Althans, zo begrijp ik het. Ik heb een keer een poging gedaan om een cursus Einstein’s field equations te volgen, maar ik heb al rap de handoek in de ring gegooid 🙂 Ik wil maar zeggen……
LOL…K.J. Die van die Schotse proffessor op Youtube? 1 Uur en 45 minuten ! Bij mij kwam de stoom na 29 minuten al uit mij oren.
Nee niet dat ???? Zijn video’s zijn nog redelijk te volgen. Ik bedoelde deze online cursus https://www.coursera.org/learn/general-relativity
Er zijn er twee over dit onderwerp die me wel lukte, oftewel je hoeft niet bijzonder slim te zijn om ze te kunnen volbrengen ????
https://www.coursera.org/learn/einstein-relativity
en
https://www.edx.org/course/einstein-revolution-harvardx-emc2x-0
Nee veel erger, die schot (ook goede video’s trouwens) is er nog een lievertje bij 🙂
Ik bedoelde deze; https://www.coursera.org/learn/general-relativity
Deze:
https://www.youtube.com/watch?v=foRPKAKZWx8
Óok een prachtige site:
https://www.pitt.edu/~jdnorton/teaching/HPS_0410/chapters/general_relativity_pathway/index.html