
De Hubble eXtreme Deep Field (XDF). Credit: NASA, ESA, H. Teplitz and M. Rafelski (IPAC/Caltech), A. Koekemoer (STScI), R. Windhorst (Arizona State University), and Z. Levay (STScI).
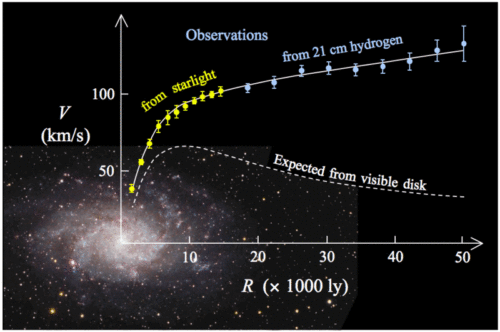
Poincaré, Kapteyn, Oort en Zwicky kwamen als eersten aanzetten met het idee van donkere materie (in de jaren tien, twintig en dertig van de vorige eeuw), maar het was vooral door de waarneming van de vlakke rotatiecurves van sterrenstelsels door Vera Rubin in de jaren zeventig van de vorige eeuw dat de theorie van de donkere materie vaste grond kreeg (zie de afbeelding hieronder).
Naast die vlakke rotatiecurves kwamen er nog meer indirecte observationele bewijzen voor het bestaan van donkere materie, het mysterieuze spul dat 85% van alle materie in het heelal zou vormen: zwaartekrachtlenzen, de Bullet cluster én de pieken in het ‘Power spectrum’ van de kosmische microgolf-achtergrondstraling. Alleen één ding ontbreekt nog, de ‘smoking gun’ van donkere materie, de directe waarneming ervan. Ondanks tientallen experimenten over de hele wereld is nog geen gram direct waargenomen van donkere materie. Vandaar dat alternatieven voor de donkere materie de kop op blijven steken, sinds de jaren zeventig de MOND (Modified Newtonian Dynamics) en recent nog de RelMOND theorie, die het alemaal zoeken in een alternatieve zwaartekrachtwet. En nu komt er een nieuw alternatief uit onverwachte hoek aanwaaien: Alexandre Deur (University of Virginia) komt namelijk in dit vakartikel aanzetten met de suggestie dat het helemaal niet nodig is om de waarnemingen zoals de vlakke rotatiecurves te verklaren met het bestaan van donkere materie of alternatieve zwaartekrachttheorieën. Met dé vigerende zwaartekrachttheorie, de uit 1915 stammende Algemene Relativiteitstheorie (ART) van Albert Einstein, lukt dat namelijk ook.
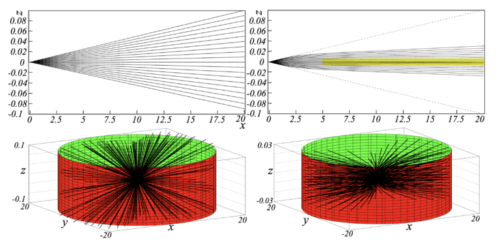
Gravitatieveldlijnen (3D en geprojecteerd) voor een schijf van de melkweg. De linkerpanelen tonen de veldlijnen zonder rekening te houden met veld-zelfinteractie. De rechterpanelen tonen de veldlijnen met zelfinteractie. Het is duidelijk dat de veldlijnen worden vervormd door het effect van zelfinteractie. Een dergelijk verschil tussen de Algemene Relativiteitstheorie en de zwaartekracht van Newton is duidelijker bij een grotere straal. Credit: Alexandre Deur.
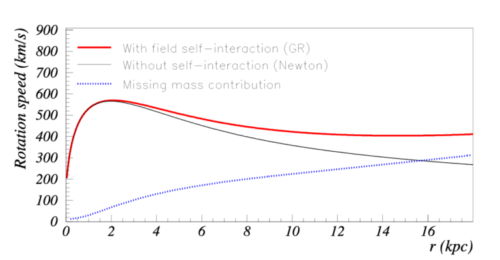
Deur zegt dat als rekening wordt gehouden met het effect van de zogeheten field self-interaction dat dan de waarnemingen verklaard kunnen worden. Zwaartekracht is in de ART non-lineair en dat betekent volgens Deur dat die zelf-interactie van het zwaartekrachtveld niet verwaarloosd mag worden. De vlakke rotatiecurven ontstaan allemaal bij lage snelheden, dus relativistische effecten, die je bij de lichtsnelheid verwacht, zijn niet aan de orde. Deur rekent in z’n artikel uit dat door de zelf-interactie van het zwaartekrachtsveld de zwaartekracht sterker wordt dan in de Newtoniaanse zwaartekracht geldt, die bij lagere snelheden optreedt. Op grond van de zelf-interactie van de zwaartekracht in de ART komt Deur met deze grafiek van de rotatiecurve van een sterrenstelsel (de rode lijn is zijn berekening):
Mmmmm, de zelf-interactie van zwaartekracht als alternatief voor donkere materie of (Rel-)MOND. Je zou toch denken dat zo’n simpele suggestie eerder al zou zijn gedaan? Hebben we zitten slapen of is er toch één of andere denkfout in de theorie van Deur? We gaan ’t zien. Bron: Astrobites.



Gets my vote.
Alles wat aan de poten zaagt van donkere materie krijgt mijn stem 🙂
De vergelijkingen van de algemene relativiteitstheorie (ART) zijn zeer ingewikkeld. Anderzijds zijn er geavanceerde algoritmes die polynomiale vergelijkingen goed kunnen benaderen, zeker wanneer die algoritmes in een geavanceerde computer worden geprogrammeerd. Het lijkt me dat een lineaire benadering (met alleen 1e machtstermen) niet voldoet, veel te simpel. Het is zaak om nu een hypothetisch sterrenstelsel met een dikke schijf met cirkelsymmetrie goed door te rekenen (qua zwaartekracht) tot op de hogere machtstermen in de ART.
Dan zal snel blijken of deze stelling van Duer klopt of niet.
“Eerst op een telraam, dan op een computer”
Citaat van een oom van me.
Gezien de dalende trend in zijn berekende rode lijn t.o.v. de stijgende uit de waarnemingen tot 16 kpc (visueel sterrenlicht) schiet het niet hard op met zijn theorie. Ik zie dat zijn rotatie snelheid piekt op 600 km/s en die van Rubin e.a. maar tot 100 – 150 km/s komt… ra ra. En de vraag blijft waarom alle roterende sterrenstelsels zijn gebonden aan die vaste rotatiesnelheid van 1 miljard jaar per omwenteling ongeacht hun diameter en die impuls dus blijkbaar al meekregen ten tijde van hun ontstaan.