In 1998 ontdekten twee wetenschappelijke teams onafhankelijk van elkaar dat het heelal versneld uitdijt. De uitdijing van het heelal kenden we al sinds eind jaren twintig van de vorige eeuw dankzij Lemaître en Hubble, de versnelling kennen we dankzij Perlmutter, Riess en Schmidt. Om de snelheid van de uitdijing weer te geven hanteren de sterrenkundigen de Hubble constante HO, de evenredigheidsfactor in de wet van Hubble – Lemaître:
$latex v=H_{0}\,D$
Feitelijk is HO geen constante, maar is het de waarde van de Hubble parameter op dit moment. Hoe groot H0 is dat is niet bekend, hij zit ergens tussen ruwweg 68 en 73 km/Mpc, twee waarden waar de bekende Hubble spanning om draait. De Hubble parameter is in 1922 al door de Rus Alexander Friedmann beschreven (schrik niet van de vergelijkingen):
$latex {\displaystyle H^{2}\equiv \left({\frac {\dot {a}}{a}}\right)^{2}={\frac {8\pi G\rho +\Lambda }{3}}-K{\frac {c^{2}}{a^{2}}}}$
$latex {\displaystyle 3\,{\frac {\ddot {a}}{a}}=\Lambda -4\pi G\left(\rho +{\frac {3p}{c^{2}}}\right)}$
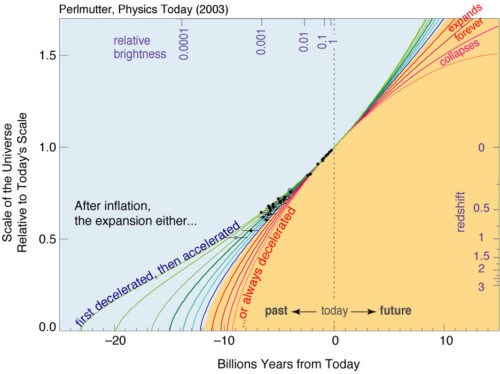
De formules maken duidelijk dat de kromming van de ruimte van het heelal bepaald wordt door een mix van factoren, met name de druk, zwaartekracht en dichtheid van massa en energie. In de vergelijkingen is a de zogeheten schaalfactor van het heelal, een dimensieloze factor, die ook wel de kosmische schaalfactor of de Robertson Walker schaalfactor wordt genoemd. Dit is een maat voor hoeveel keer het heelal is uitgebreid. Per definitie is a op dit moment 1, dus als a=2 betekent het dat het universum twee keer zo veel is uitgedijd als nu. En als a=0,5 betekent het dat het heelal slechts half zo veel was uitgedijd als nu. Afhankelijk van de factoren kan volgens de Friedmann vergelijkingen de toekomst van het heelal open, gesloten of vlak zijn. Dat hebben ze sinds de jaren negentig proberen te meten en de uitkomst zie je in de afbeelding hieronder – ten tijde van de oerknal was a=0.
Duidelijk is dat het heelal na de inflatie eerst vertraagde in tempo van uitdijing en daarna versnelde. De Hubble parameter, die deze verandering beschrijft, verandert met de tijd en sinds de oerknal 13,8 miljard jaar geleden is ‘ie gedaald. In de evolutie van het heelal zijn enkele periodes te onderscheiden, waarin het tempo van deze uitdijing van het heelal varieerde:
- Inflatieperiode: zeer kort na de oerknal vindt er een kortstondige periode aan van exponentiële uitdijing van het heelal.
- Stralingsgedomineerde periode: na de inflatieperiode is er een periode waarin de dynamica van het heelal bepaald wordt door straling. Dit duurt tot 47.000 jaar na de oerknal. Tijdens deze periode verandert de schaalfactor als volgt (waarbij de schaalfactor a een functie is van de tijd t): a(t) ∝ t¹/².
- Materiegedomineerde periode: deze duurt tot ca. 9 miljard jaar na de oerknal én in deze periode werd de dynamica bepaald door materie. Tijdens deze periode verandert de schaalfactor als volgt: a(t) ∝ t²/³.
- Donkere energiegedomineerde periode: vanaf ongeveer 9 miljard jaar na de oerknal wordt de donkere energie dominant. Omdat deze een afstotende werking heeft is het gevolg dat het heelal versneld uitdijt. Tijdens deze periode verandert de schaalfactor als volgt: $latex {\displaystyle a(t)\propto \exp(H_{0}t)}$.
Nou zou je verwachten dat een heelal dat een versnelde uitdijing kent, zoals de laatste vier miljard jaar het geval is, een Hubble parameter heeft die toeneemt. Maar het omgekeerde is het geval: H is afgenomen sinds de oerknal én hij blijft dat doen, óók tijdens de periode van versnelde uitdijing. De verklaring is nogal technisch van aard. De Hubble parameter kan ook worden beschreven als:
$latex {\displaystyle H(t)\equiv {\dot {a}}(t)/a(t)}$
Zoals eerder gezegd is a per definitie op dit moment 1, bij t=0 (oerknal) was a ook 0. De stip op de a geeft aan dat $latex {\dot {a}}$ een tijdsafgeleide betreft, het geeft de verandering van de snelheid van de uitdijing van het heelal aan. En om het nog ingewikkelder te maken is er ook nog een tweede afgeleide van de schaalfactor, dat is ä, de verandering van de verandering (je ziet ‘m in de tweede Friedmann vergelijking). Het is ä die positief is en dat zorgt ervoor dat ze sprekend van een versnelling van de uitdijing van het heelal. De schaalfactor a en de afgeleide $latex {\dot {a}}$ zijn ook positief. Zoals gezegd is a=1 en die wordt groter naarmate het heelal uitdijt, met a->oneindig als limiet. En nou komt het: a neemt sneller toe dan $latex {\dot {a}}$, dus krijg je dat H dan afneemt (per slot van rekening is bij $latex {\dot {a}}$/a de deler groter dan de noemer). Dus zelfs met een versnelde uitdijing van het heelal (door een positieve ä) daalt H. Dat zal niet eeuwig blijven dalen tot 0, H zal volgens berekening dalen tot de asymptotische limiet
$latex H(\infty) = H_0\sqrt{\Omega_{\Lambda,0}}$
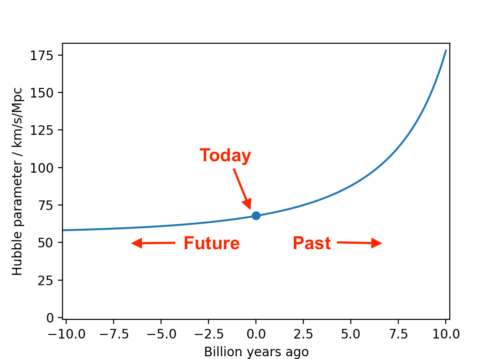
waarin ΩΛ,0 de dichtheid van donkere materie is. Nemen we voor ΩΛ,0 0,663 (zie deze laatste meting) dan krijgen we bij H0=67,4 een H(∞) van ≈54,8 km/s/Mpc en bij bij H0=73,5 een H(∞) van ≈59,8 km/s/Mpc. Als die limiet bereikt is daalt H niet verder en zal het heelal met dat tempo voor eeuwig verder uitdijen (zie de grafiek hieronder).
Hoe snel die afname van H gaat? Die is pakweg:
$latex dH/dt \simeq -1.2\,\mathrm{km}\,\mathrm{s}^{-1}\,\mathrm{Mpc}^{-1}\,\mathrm{Gyr}^{-1}$
Dus ruwweg een miljard jaar voor een daling met 1 km/s. Ik kwam afsluitend ergens de volgende metafoor tegen, die gaat over de ogenschijnlijk tegenstrijdigheid van een dalende Hubble parameter en een versnellende uitdijing van het heelal:
Het universum gedraagt zich als een rivier met stroomversnellingen. Als je een boot in de rivier zet en hem door de stroming laat meevoeren, zal hij versnellen terwijl hij stroomafwaarts vaart en de stroomversnellingen binnengaat. Maar als je op de oever zit en de snelheid van het water op één locatie meet, verandert deze op basis van een geheel andere reeks factoren – bijvoorbeeld de snelheid waarmee de watertoevoer van stroomopwaarts verandert. Het is mogelijk dat de watersnelheid op uw locatie in de loop van de tijd afneemt, ook al versnelt elke boot die u loslaat terwijl deze de stroomversnellingen invaart. Bron: Cornell.





Een variabele Hubble constante zou kunnen leiden tot meer invloed van toenemende rood verschuiving door variabele lightnsnelheden in het vroege heelal door meer zwarte gaten. : zie: https://bigbang-entanglement.blogspot.com/2022/05/what-was-before-big-bang-big-crunch-in.html
Waarom waarschuwt Google voor jouw blog Leo?
Die versnelde uitdijing is gebaseerd op metingen aan het type Ia supernovae die voorheen geacht werden te bestaan uit een homogene groep. Daaraan wordt al een tijdje gezaagd en zou dus kunnen betekenen dat het onderzoek zou moeten worden overgedaan, zie https://www.nobelprize.org/prizes/physics/2011/perlmutter/biographical/ en https://nl.wikipedia.org/wiki/Supernova_type_Ia . Citaat: “Niet zo lang geleden zijn wetenschappers erin geslaagd aan te tonen dat type Ia-supernovae, die altijd als homogeen beschouwd zijn, in feite niet geheel aan elkaar gelijk zijn.[50] Hierbij wordt gesteld dat het type Ia dat vandaag de dag vrij zeldzaam is, in het vroegere universum veel vaker voorkwam.[51] Deze relatief nieuwe ontdekking kan weleens verstrekkende gevolgen hebben voor de fysische kosmologie, zoals een mogelijke revisie van de snelheid van de uitdijing van het heelal en de kracht van de mysterieuze donkere energie. Ook is het voer voor het debat over de Hubble-spanning.[52]” Het zou dus m.i. zomaar kunnen dat het universum wel uitdijt maar niet meer versneld (dat strijdig is met alle logica) en wellicht vervalt dan ook de Hubble spanning met een beetje selectie…..
De type Ia supernovae kwamen in het vroege heelal vaker voor dan tegenwoordig, dat zou best het geval kunnen zijn. Per slot van rekening was er vroeger meer stervorming en daarmee had je ook meer sterren die uiteindelijk als type Ia SNe eindigden. De vraag is alleen of er ook een fysiek verschil was tussen de vroege en huidige type Ia SNe. Zo niet dan is er alleen een kwantitatief verschil en maakt het niet uit voor de afstandsmetingen.
Het ziet er allemaal goed onderbouwd uit door mr Pinto https://www.slac.stanford.edu/econf/C0307282/lec_notes/pinto/pinto.pdf . Maar hier een recent artikel (2022) die toch twijfel probeert te zaaien. https://www.scirp.org/journal/paperinformation.aspx?paperid=110989