Credit: ESA/Hubble, Digitized Sky Survey, Nick Risinger (skysurvey.org), N. Bartmann
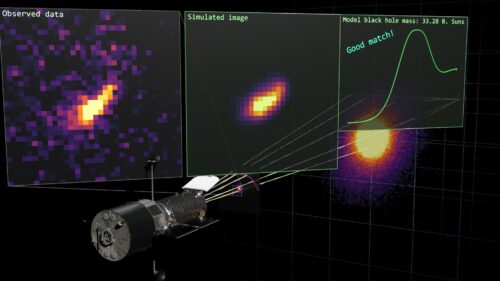
Een team van sterrenkundigen is er in geslaagd om met behulp van een zwaartekrachtlens een kolossaal zwaar zwart gat te ontdekken, eentje die maar liefst 32 miljard keer zo zwaar als de zon is. Het team, dat onder leiding stond van James Nightingale (Durham University), vond het superzware zwarte gat door waarnemingen aan een sterrenstelsel ruim twee miljard lichtjaar van ons vandaan, een stelsel dat deel uit maakt van een cluster van sterenstelsels, Abell 1201. Het stelsel vormt door zijn massa een natuurlijke lens, waardoor het licht van een sterrenstelsel dat gezien vanaf de aarde precies achter het voorgrondstelsel gelegen is afbuigt en wordt versterkt. Dat effect wordt een zwaartekrachtlens genoemd, iets dat door Albert Einstein op grond van z’n Algemene Relativiteitstheorie meer dan honderd jaar geleden al werd voorspeld. Het centrale elliptische cD stelsel in het midden van Abell 1201 vormt zo’n zwaartekrachtlens en deze is met de Hubble ruimtetetelecoop nauwkeurig gefotografeerd.
Vervolgens is men aan de slag gegaan met simulaties op de computer om te kijken welke massa het zwarte gat in het cD stelsel moet hebben om tot de waargenomen vorm van de zwaartekrachtlens te komen. Die simulaties werden uitgevoerd op de DiRAC COSMA8 supercomputer van de universiteit van Durham en daarbij heeft men wel honderduizenden simulaties gedaan met telkens wisselende massa’s om te kijken welk lichtpad het achtergrondstelsel gevolgd heeft bij die specifieke massa. De uitkomst was dat toen een massa van 32 miljard zonsmassa voor het zwarte gat werd gebruikt de simulatie exact overeenkwam met de door Hubble gedane waarneming. Het is voor het eerst dat men de massa van een superzwaar zwart gat heeft bepaald met behulp van een zwaartekrachlens. Normaal zijn superzware zwarte gaten erg actief doordat ze massa aantrekken en dan geven ze straling af die gemeten kan worden en die iets zegt over hun massa. Maar met deze methode kunnen ook ‘stille’ superzware zwarte gaten worden gemeten.
Fregment uit de simulatie met de juiste massa. Credit: Durham University
Meer informatie vind je in het vakartikel van James Nightingale et al, Abell 1201: Detection of an Ultramassive Black Hole in a Strong Gravitational Lens, Monthly Notices of the Royal Astronomical Society (2023).
Bron: Phys.org.
Geweldig toch dat het universum ons natuurlijke telescopen levert met het formaat van miljarden lichtjaar!
De reden dat men zo het zwarte gat kon “wegen”, dus zonder de massa van het hele stelsel erbij, is dat het gelensde beeld (beeld van het achtergrondstelsel) t.o.v. het galactisch centrum van de lens (het stelsel in het midden van Abell 1201) een schijnbare afstand van 1 kpc heeft, zo’n 3000 lichtjaar. Dat beeld hangt voor ons dus vrijwel naast het centrum. Hoe verder naar buiten dat beeld staat, hoe lastiger de massa van slechts het centrale zwarte gat te meten wordt.
De massa is een upper limit: het zal nog wel wat naar beneden worden bijgesteld, want een bol met een straal van 1 kpc in het centrum van een stelsel bevat nog best veel materie. Een grove schatting voor het centrum van de Melkweg levert een verhouding van ongeveer 1:4 op, dwz, 4 keer meer massa in een volume van 1kpc t.o.v. het zwarte gat aldaar (of beter: de schatting voor dat volume is 16 miljoen solar mass incl. de massa van Sgr A*).
Zou zo´n gravitatielens ook last van chromatische Aberratie hebben? Immers de equivalente massaenergie (h.f) van de fotonen bepalen m.i. de deviatie van de rechte lijn. Dat zou dan weer betekenen dat de berekende massa van deze BH afhankelijk is van de gekozen frequentie in het EM spectrum. Of sla ik nu de Planck mis?
Dat lijkt me niet. Zwaartekracht is geen medium zoals een normale lens en alle fotonen, ongegacht hun golflengte, worden even sterk afgebogen in een zwaartekrachtveld. Er kunnen via verschillende geodeten wel meerdere beelden gelensd worden, maar die beelden zijn niet geordend op golflengte.
“Immers de equivalente massaenergie (h.f) van de fotonen bepalen m.i. de deviatie van de rechte lijn”
Een geodeet is in wezen een rechte lijn, alle fotonen volgen de geodeet en die met korte golflengtes zullen daar niet meer van afbuigen dan fotonen met langere golflengtes.
Klopt inderdaad! Geen enkele verwijzing hier in de link naar de virtuele massa van het foton in deze brij van formules 😀 . De ideale lens dus zonder artefacten. Ik vond het al zo vreemd dat de projecties zo scherp bleven. https://profoundphysics.com/how-are-photons-affected-by-gravity-if-they-have-no-mass/ Weer wat opgestoken…
Goede link.
Het concept van relativistische massa is verwarrend (mijn aanname is dat je dit bedoelt met ‘virtuele massa’). De massa van een object op hoge snelheid verandert niet, maar de weerstand om te veranderen (inertia/traagheid) doet dat wel. Kinetische energie ondergaat traagheid zoals alle vormen van energie. Acceleren is verandering. Meer snelheid = meer kinetische energie = meer traagheid = meer energie nodig, etc.
Kinetische energie graviteert ook, net als meer massa, dus de verwarring ligt om de hoek: ik zie meer snelheid, ik zie meer zwaartekracht, dus de massa moet ook toegenomen zijn. Maar onjuist: meer kinetische energie = meer zwaartekracht.
Misschien vind je deze uitleg interessant:
https://bigthink.com/hard-science/light-speed-relativistic-mass/
Ik ben dus ook jaren lang misleidt begrijp ik hieruit: “The key message — beyond the one that while inertia does increase with speed, mass remains the same — is that it is easy for intelligent people to be misled by simplified explanations for complex problems.” We zitten plotseling met een verborgen variabele y die varieert tussen 1 en oneindig door een simplificatie van E=MC^2 😀
voorbeeld: https://natuurkundeuitgelegd.nl/videolessen.php?video=rustmassa#:~:text=De%20massatoename%20is%20zelfs%20zo,om%20de%20lichtsnelheid%20te%20bereiken. Fout dus begrijp ik nu. Overal op internet staat dus verkeert uitgelegd dat de massa van deeltjes (m.u.v. bosonen) oneindig wordt bij de lichtsnelheid. Maar wat is de oorzaak van die inertia wil je dan weten. “The inertia is the result of the initial resistance between the moving bodies against the static vacuum. The moving body drags the resisting vacuum during acceleration, till the point that the vacuum travels with the moving body and has the same velocity.” Dat schiet niet erg op… een meebewegend vacuum gevuld met vacuumenergie en virtuele deeltjes die nota bene ook nog de lichtsnelheid bepalen?
bron: https://www.scirp.org/journal/paperinformation.aspx?paperid=108888 Dat gaan we eens rustig lezen t.z.t. 😀