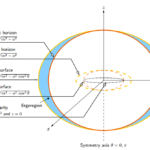
Eerste foto van zwart gat, M87*. (c) EHT Collaboration.Het 6,5 miljard zonsmassa wegende zwarte gat M87*, te vinden in het centrum van het enorme elliptische stelsel M87 in het midden van de Virgocluster van sterrenstelsels, waarvan we op 10 april voor het eerst de foto zagen, is een Kerr zwart gat. … [Lees meer...]
M87* is een Kerr zwart gat en dat geeft ‘m best wel bijzondere eigenschappen
22 april 2019 door Reageer
Mag ik even voorstellen: de Buchdahl limiet, de laatste halte vóór de vorming van een zwart gat
7 november 2016 door 11 Reacties
Om een zwart gat te krijgen is een lange weg te gaan. Het zijn de meest compacte objecten in het heelal, zo compact zelfs dat hun kern, hun singulariteit zoals dat heet, niet beschreven kan worden met de twee grootste natuurkundige theorieën van de twintigste eeuw, de relativiteitstheorie en de … [Lees meer...]