 Interessante vraag voor het spel Triviant [1]Of is het nou Trivial Pursuit?: is er een absolute maximumtemperatuur? We kennen allemaal het absolute nulpunt: de temperatuur van 0 kelvin of van -273,15 °C. Kouder kan niet, want dan zouden de atomen volkomen stilstaan en dat kan niet. Maar is er ook zoiets als het absolute maximum? Op die vraag blijkt door de natuurkundigen verrassend genoeg niet één eenduidig antwoord te kunnen worden gegeven. Het hangt namelijk van het gekozen model voor de natuurkrachten af welke maximum-temperatuur mogelijk is. Een paar opties:
Interessante vraag voor het spel Triviant [1]Of is het nou Trivial Pursuit?: is er een absolute maximumtemperatuur? We kennen allemaal het absolute nulpunt: de temperatuur van 0 kelvin of van -273,15 °C. Kouder kan niet, want dan zouden de atomen volkomen stilstaan en dat kan niet. Maar is er ook zoiets als het absolute maximum? Op die vraag blijkt door de natuurkundigen verrassend genoeg niet één eenduidig antwoord te kunnen worden gegeven. Het hangt namelijk van het gekozen model voor de natuurkrachten af welke maximum-temperatuur mogelijk is. Een paar opties:
Ten eerste: Volgens het standaardmodel van de elementaire deeltjes en krachten is er één absolute maximumtemperatuur, de zogenaamde Plancktemperatuur, genoemd naar de Duitse natuurkundige Max Planck. Deze bedraagt:
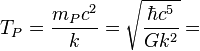 1.41679(11) x 1032 K.
1.41679(11) x 1032 K.
Best wel heet, nietwaar? 😉 Afgezien van de allereerste 10-43 seconden na de Oerknal is deze temperatuur nooit bereikt in enig object. Boven die temperatuur kunnen de huidige theoretische modellen geen verklaring geven voor hetgeen er allemaal gebeurt. Daar is dan weer die bekende Theorie van Alles voor nodig.
Ten tweede: natuurkundigen die in de snaartheorie geloven hebben een andere absolute maximumtemperatuur: de zogenaamde Hagedorntemperatuur. Goh, die is ook weer door een Duitse natuurkundige bedacht, in dit geval ene Rolf Hagedorn. De meeste snaarnatuurkundigen durven geen exact getal te noemen voor de waarde ervan, maar door een enkeling wordt 1030 K genoemd, dus twee orden van grootte kleiner dan de Plancktemperatuur. Brrrrr, koud. 🙂
Ten derde: heel praktisch wordt door een aantal natuurkundigen 1017 K genoemd. Hoe ze daaraan komen? Simpel door te kijken wat de Large Hadron Collider, de superdeeltjesversneller die dit jaar in bedrijf wordt genomen, aan temperatuur kan bereiken. En da’s die respectabele 1017 K, die nog wel 15 orden van grootte kleiner is dan de Plancktemperatuur. Er zijn modellen die voorspellen dat bij de 14 biljoen electronvolt die de LHC kan bereiken extra dimensies vrijkomen, die verhinderen dat de Plancktemperatuur gehaald wordt. De grens van 1017 K zou daarmee een absolute maximumtemperatuur kunnen zijn.
Ten vierde: heel verrassend 0 K! Er zijn natuurkundigen die denken dat het absolute nulpunt wel eens hetzelfde kan zijn als het absolute maximum. 😯 Tsja, daar moeten we een andere keer maar eens verder over discussieren. Bron: PBS.org.
Voetnoten
| ↑1 | Of is het nou Trivial Pursuit? |
|---|





Weer zo’n interessant artikel hier.
Een vraagje. Je schrijft: “het absolute nulpunt: de temperatuur van 0 kelvin of van -273,15 °C. Kouder kan niet, want dan zouden de atomen volkomen stilstaan en dat kan niet.”
Waarom kunnen atomen niet volkomen stilstaan? (niet dat ik je niet geloof, integendeel, maar ik vraag me dergelijke dingen gewoon af)
In theorie zouden atomen wel stil kunnen staan, maar in de praktijk zullen ze altijd een klein beetje bewegen, de zogenaamde nulpuntsbeweging. In laboratoria kan men atomen vrijwel tot stilstand brengen (zoals in Einstein-Bose condensaten), maar ‘vrijwel’ is niet hetzelfde als ‘helemaal’. Het is dus meer een praktische omstandigheid, dan een theoretisch verbod van dat stilstaan.
De reden zit volgens mij in het onzekerheidsbeginsel van Heisenberg, waardoor je nergens aan precies 0 kunt raken, dus ook niet bij energie. Vandaar dat men atomen niet volledig tot stilstand kan brengen.
Verder zeer interessant artikel! Ik had nog niet gehoord van de mogelijkheid van een absolute maximumtemperatuur 🙂
In dat beginsel worden Δx (de onzekerheid in de plaats) en Δp (de onzekerheid in de impuls) gerelateerd. Als een atoom volkomen stilstaat is z’n plaats exact bekend. Ik weet niet of dat betekent dat z’n impuls dan oneindig groot wordt, wel dat we in dat geval niet weten wà t de impuls is.
Geachte,
Op de website van hyperphysics staat een temperatuur die 5 orden van grootte hoger is dan de plancktemperatuur. Althans zo loopt de grafiek van hoe het heelal is begonnen. En ik leid af dat bij t=10^-52s het heelal op dat moment een temperatuur had van 10^37K!
En op Wikipedia bij ordes of magnitude staat ook een temperatuur van 10^33K, 10 keer heter dan de Plancktemperatuur, en erbij staat iets van “Landau Poles”. Ik begrijp er eerlijk gezegd nu niets meer van.
Is er een theorie die een hogere temperatuur dan de Plancktemperatuur toestaat? En wat gebeurt er dan?
En wat zijn Landau Poles?
Zou een oneindig hoge temperatuur theoretisch kunnen, zoals op t=0 bij de Big Bang?
Ik vind het verder ook een heel interessant artikel.
Die grafiek van hyperphysics (te bewonderen als je op J.Sneller’s naam klikt) is volgens mij niet helemaal correct aan de linkerzijde. Dat wil zeggen dat de tijd daarin doorloopt tot 10^-50 seconden, maar de vraag is of dat ook realistisch is. Natuurkundigen denken dat de kortste tijdseenheid de Plancktijd is (10^-43 s), dus een tijd als 10^-50 seconden na de Big Bang met de daarbij behorende hógere temperatuur dan de Plancktemperatuur, heeft misschien nooit plaatsgevonden. Ik zeg ‘misschien’, want het blijft uiteraard gissen en probleem is dat de huidige natuurwetten totaal niets kunnen zeggen over die waarden ‘voorbij Planck’. Eh.. wat die landau Poles betreft, geen idee wat dat voor dingen zijn. Ik zal mij er es in gaan verdiepen. Bedankt tenslotte voor het compliment over het artikel. 🙂
en als we nou kijken naar de formule 3/2 Kb T = 1/2 M (V^2), die ons vertelt hoe de snelheid van de moleculen samenhangt met de temperatuur, kunnen we dan niet gewoon zeggen dat de max V, C is en dat de massa van een molecuul ook niet oneindig groot kan worden, dan komen we toch ook op een limiet?
Deeltjes kunnen niet volledig stilstaan (noch in theorie noch in de praktijk). Dit komt door onzekerheidsrelatie van Heisenberg. Die verteld dat als 1 waarde wordt gemeten, de andere waarde in zijn onzekerheid steigt. Als voorbeeld: een pinpongballetje tussen je hand en de tafel (20 cm) is goed te meten in snelheid, maar zijn plaats ligt ergens tussen die 0 en 20 cm. Als deze afstand kleiner wordt gemaakt is de plaats duidelijker maar de snelheid moeilijker te meten. Zo kun je de relatie ongeveer voorstellen. Dit betekend dat de onzekerheid in de grootheid die je niet meet oneindig groot zou zijn als de grootheid die je wel meet zeer precies bekend is.
Daarom is het dus niet mogelijk (theoretisch en praktisch) om volledig stil te staan (op kwantumniveau uiteraard). De beweging die overblijft wordt inderdaad de nulpuntsbeweging genoemd.
De maximale temperatuur bedenk ik als de temperatuur waar de moleculen met de maximale snelheid bewegen (lichtsnelheid) of iniedergeval in hoeverre ze die snelheid kunnen bereiken. Dit zal wel niet juist zijn maar klinkt voor mij wel logisch.
@Jan,
Je kan niet meten dat een atoom stilstaat, maar dat wil toch niet zeggen dat het niet mogelijk is?
@Moi, Nee, het is wat Jan zegt: zowel theoretisch als praktisch is het uitgesloten dat een atoom compleet stilstaat. Je krijgt de Nobelprijs voor de natuurkunde als je het tegendeel kan bewijzen. Succes d'r mee. 😀
als de absolute temperatuur oneindig zou zijn zouden de moleculen de lichtsnelheid overschrijden.
tenzij dat kan (wat nog niet zeker is) is het onmogelijk om de maximumtemperatuur op oneindig te stellen.
maar wat zou de temperatuur zijn als moleculen op lichtsnelheid bewegen?
wat de massa betreft, dat worden dan allemaal elementen, die moleculen die uit meer dan een atoom bestaan zouden zeker uit elkaar vallen, maar de vraag is dan weer of de kernen versmelten en er energie verloren gaat aan radioactiviteit (verval van die kernen).
Hoe dan ook, in 3 van de 4 gevallen kan je dus behoorlijk je jatten branden 🙂
In het vierde geval branden de natuurkundigen hier aan hun jatten 🙂