Zoals ik ooit wel eens heb gezegd, houd het Higgsboson verband met de zwakke kernkracht. Zoals beloofd, zal ik hier verder op ingaan. Hoewel de ontdekking van het Higgsboson overal de voorpagina gehaald heeft, hebben we feitelijk driekwart van de Higgs al veel eerder ontdekt. Driekwart van de Higgs is namelijk opgegeten door beesten die Z-en W-bosonen [1]zij zijn de overdragers van de zwakke kernkracht, één van de vier fundamentele natuurkrachten genoemd worden. Maar wat is in vredesnaam driekwart van een deeltje? Wat heeft de Higgs van doen met Z- en W-bosonen? En hebben we nu wel of niet de Higgs ontdekt?Het verschil tussen massieve en massaloze vectorbosonenEr is namelijk niet een ‘echte’ Higgs – volgens het Standaard Model zijn er maar liefst vier Higgsen. Drie ervan worden geabsorbeerd door W- en Z-bosonen en de vierde is degene die we de Higgs noemen. Kijk, het zit zo: krachtoverbrengende deeltjes (vectorbosonen) hebben een eigenschap die spin genoemd wordt en deze spin resulteert in polarisatiestaten. Zo’n polarisatie is een bepaalde manier waarop een kwantumdeeltje kan spinnen en iedere polarisatiestaat vertegenwoordigt feitelijk een afzonderlijk deeltje, of eigenlijk een onafhankelijke “mate van vrijheid”. Op die manier zijn er twee soorten fotonen [2]lichtdeeltjes – de overbrengers van de elektromagnetische kracht: de ene draait linksom en de andere draait rechtsom. Theoretisch gezien zouden er nog twee polarisatiestaten van licht moeten zijn, want een foton heeft immers nog twee ‘richtingen’ over. Toch kan een foton niet spinnen in de richting waarin het beweegt, want dan zou een gedeelte van het elektromagnetische veld sneller reizen dan het licht en dat is dus verboden.Okee, zover is het hopelijk duidelijk. Uit bovenstaande kan afgeleid worden dat deeltjes met massa wél kunnen spinnen in de bewegingsrichting. Zij hebben dus een extra ‘mate van vrijheid’ in vergelijking met massaloze deeltjes. Nu hebben zowel het foton als het gluon (de overbrenger van de sterke kernkracht) geen massa, terwijl de W- en Z-bosonen wél massa hebben. Onthoud het volgende:
“Het verschil tussen massaloze krachtdeeltjes (zoals fotonen en gluonen) en massieve krachtdeeltjes (zoals de W en Z) is de longitudinale mate van vrijheid”
Aangezien iedere mate van vrijheid zich ongeveer gedraagt als een onafhankelijk deeltje, zeggen we feitelijk het volgende: de W en Z hebben een extra ‘deeltje’ in zich in vergelijking met fotonen en gluonen. De massa van een krachtdeeltje is sowieso erg belangrijk voor de natuurkunde en dé reden dat Maxwell zijn klassieke theorie van elektromagnetisme kon ontwikkelen: het foton heeft geen massa en produceert dus een macroscopisch krachtveld, terwijl de W en Z erg zwaar zijn en slechts op zeer korte (microscopische) afstand hun invloed kunnen laten gelden. Het kost deeltjes veel energie om massieve krachtoverbrengende deeltes uit te wisselen 😉
Massieve vectors zijn een probleem
Het feit dat zowel de W als de Z massief zijn is om de volgende reden belangrijk:
“In de vroege dagen van de kwantumveldtheorie sloeg het concept van massieve vectordeeltjes helemaal nergens op”
De details doen er even niet toe, maar het gaat erom dat de wiskundige consistentie van een theorie met massieve vectordeeltjes z’n geldigheid verliest bij hoge energieën. Je zou bijvoorbeeld de volgende vraag kunnen stellen: hoe groot is de kans dat W-deeltjes elkaar verstrooien? Dat is een prima en goed doordachte natuurkundige vraag, maar zodra je ‘m stelt realiseert de theorie zich plotseling dat er iets niet klopt en kapt-ie ermee 😛 Het is bijna alsof massieve vectordeeltjes simpelweg niet zijn toegestaan.Als dat het geval is, hoe kunnen W- en Z-bosonen dan massa hebben? Krachtoverbrengende deeltjes verschijnen in theorieën altijd als massaloze deeltjes. We hebben inmiddels gezien dat het verschil tussen een massaloos en een massief deeltje een extra, longitudinale mate van vrijheid is. We moeten dus een manier vinden om een extra mate van vrijheid te geven aan de W en de Z.
Wie lust er een Goldstone-boson?
Okee, waar kan deze extra mate van vrijheid vandaan komen? Een mooie oplossing voor deze puzzel is het Higgs-mechanisme. Het komt erop neer dat vectordeeltjes simpelweg een ander deeltje kunnen annexeren om een “extra deeltje aan vrijheid” te verkrijgen (m.a.w. om massief te worden – dit is overigens iets heel anders dan hoe andere deeltjes via de Higgs hun massa verkrijgen!)Okee, maar wat voor extra deeltjes zijn hiervoor nodig? Aangezien deeltjes met spin slechts twee “mates van vrijheden” hebben, kan deze extra longitudinale mate van vrijheid alléén afkomstig zijn van een deeltje zónder spin! Een dergelijk deeltje wordt een scalair deeltje genoemd en zou op de één of andere manier verbonden moeten zijn met de zwakke kernkracht om door de W en Z opgegeten te worden. Dat betekent dat ze een zogenaamde zwakke lading dienen te hebben.Hiermee bedoel ik niet dat de lading zwak is, maar dat het een lading is dat verbonden is met de zwakke kernkracht. Net zoals deeltjes een elektromagnetische lading kunnen hebben (het soort lading waar je meestal aan denkt als je ‘lading’ hoort in een natuurkundige context 😛 ), kunnen deeltjes ook een ander soort lading hebben. Neem neutrino’s eens als voorbeeld: die zijn ongeladen in de elektromagnetische kracht, aangezien ze niet met fotonen praten. Ze zijn wél geladen in de zwakke kernkracht, aangezien ze wél met W- en Z-bosonen praten!Anyway, deeltjes die gecombineerd kunnen worden met massaloze krachtdeeltjes om massieve krachtdeeltjes te maken worden Goldstone-bosonen genoemd. Het Goldstone-theorem zegt dat
“Iedere theorie met een spontane symmetriebreking een massaloos scalair deeltje in z’n spectrum heeft”
Nou, da’s mooi om te weten: in theorie zouden er dus scalaire deeltjes moeten zijn. We richten ons later op de details, maar op dit moment is het voldoende om te weten dat deze scalaire deeltjes, de Goldstone-bosonen, precies het soort scalaire deeltjes zijn die door massaloze deeltjes geabsorbeerd kunnen worden om massa te verkrijgen. Dat leidt dus tot het volgende zinnetje op onze serie wandtegels:
“Krachtdeeltjes kunnen Goldstone-bosonen opeten om massief te worden”
Het sprookje van de vier Higgsen
Okee, nu gaat het ingewikkeld worden en ik hoop dat ik het kan uitleggen. Arie is eigenlijk beter in dit soort dingen, maar vooruit, komt-ie :POkee, we hebben dus drie massieve krachtdeeltjes (ook wel ijkbosonen genoemd): de W+, de W- en de Z. Deze deeltjes hebben allemaal twee extra polarisatierichtingen (links en rechts) plus een longitudinale polarisatie. Dat betekent dat we dus ook drie Goldstone-bosonen nodig hebben om ze alledrie te voeden. Waar komen die deeltjes vandaan? Je raad het al: de Higgs. Het is bijna alsof ik als een vertegenwoordiger het Standaard Model probeer te verkopen 😛
“Als je het nu koopt, krijg je bij het Standaard Model niet één, niet twee, zelfs niet drie, maar….vier – u hoort het goed – vier Higgsbosonen! Zolang de voorraad strekt!”
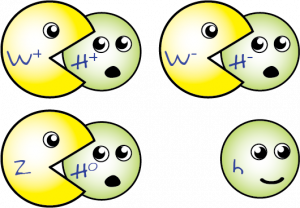
Vier Higgsbosonen? Dat klinkt als een overdosis Higgs. Maar het blijkt dat we dat precies tot beschikking hebben! We noemen ze de H+, H-, H0 en h. Zoals je kunt zien, zijn twee ervan geladen en de andere twee niet. Je kunt wel raden welke tot voedsel gaan dienen voor de W’s! (Hint: de H- en H+) Hier, ze stellen zich even aan je voor:
Lief stel hé 😛 – maar waar komen ze vandaan? En waarom zijn het er precies genoeg? Dat komt doordat de vier Higgses allemaal manifestaties zijn van een soort van overtolligheid die ijksymmetrie genoemd wordt. De naam houdt verband met ijkbosonen, de naam die we aan krachtoverbrengende deeltjes gegeven hebben.Als we vectordeeltjes beschrijven, dan zal onze wiskundige structuur tot overtolligheden gaan leiden. Kijk, in theorie hebben deeltjes vier bewegingsrichtingen, dus bevat de theorie een overtolligheid: in de parktijk hebben deeltjes 2 of 3 bewegingsrichtingen. het verschil tussen de tweede en de derde bewegingsrichting hebben we inmiddels uitgebreid beschreven: alleen deeltjes met massa kunnen in de derde, longitudinale richting bewegen. Maar hoe zit het met de vierde richting? We moeten dus nog een polarisatie verwijderen. Deze overgebleven overtolligheid is nu precies wat verbroken wordt in ijksymmetrie.IJksymmetrie verklaart niet alleen de overtolligheid in vectordeeltjes, maar zorgt ook ervoor dat een overtolligheid wordt opgelegd aan alle deeltjes die geladen zijn met de natuurkracht in kwestie. De ijksymmetrie die samenhangt met de zwakke kernkracht vereist daarom dat de Higgs uit twee componenten moet bestaan. Die twee componenten worden beschreven met een complex nummer, en aangezien complexe nummers uit twee echte nummers bestaan, is de Higgs dus opgedeeld in vier afzonderlijke deeltjes – de deeltjes die we zojuist ontmoet hebben ;)Nou, laten we nogmaals kijken naar de omschrijving van de Goldstone-theorem:
“Iedere theorie met een spontane symmetriebreking heeft een massaloos scalair deeltje in z’n spectrum”
Okee, we zijn inmiddels vertrouwd met de implicaties van een scalair deeltje. Laten we nu de rest van die zin eens gaan analyseren. Een zin die ingewikkeld wordt gemaakt door de spontane symmetriebreking. Dat idee verdient eigenlijk een eigen blog, maar in ons geval (het Standaard Model) “breken” we de ijksymmetrie die samenhangt met de W- en Z-bosonen.Kijk, wat er gebeurt is het volgende: één van de vier Higgsen (h, oftewel “dé” Higgs) krijgt een vacuum-verwachtingswaarde. Wat dat precies is, laat ik even achterwegen. Maar het impliceert dat het Higgsveld overal in de ruimtetijd “aan” staat. De Higgs draagt echter een zwakke kernlading – dus als het overal “aan” staat, dan moet iets “gebroken/verbroken” worden in deze specifieke ijksymmetrie…..aangezien het universum niet langer symmetrisch is, want er is een voorkeurs-zwakke lading…die van de Higgs, h.Okee, vanwege redenen die ik even achterwege laat (mijn brein is moe) impliceert Goldstone’s theorem dat de andere Higgsen dienstdoen als Goldstone-bosonen. Oftewel, de H+, H- en H0 kunnen opgegeten worden door respectievelijk de W+, W- en Z-bosonen, die zo de derde polarisatiestaat leveren die noodzakelijk is voor een massief vectordeeltje (en op een manier die wiskundig consistent is met hoge energieën).
Samenvatting
Pff…ingewikkelde materie, ik kan niet anders zeggen. We hebben veel opgestoken, dat is zeker, maar ik heb ook heel veel nog niet uitgelegd. Waarom er bijvoorbeeld voor ieder zwaar krachtdeeltje een afzonderlijk Goldstone-deeltje is en waarom ieder Goldstonedeeltje dezelfde lading heeft als het deeltje waardoor ze opgegeten worden. Om nog maar te zwijgen over waarom fotonen massaloos zijn, terwijl hun neefjes W en Z massa verkrijgen. Immers, waarom zou het foton niet gewoon z’n gang kunnen gaan en de h verorberen? Wat we wél gedaan hebben is uitleggen wat ijksymmetrie is en hoe de Higgs verband houdt met de massa van krachtdeeltjes. We hebben gezien dat de Higgs massa geeft aan vectorbosonen op een hele andere manier dan hoe de Higgs massa geeft aan fermionen (elektronen, protonen, etc). Fermionen “eten” nooit een deel van de Higgs, maar worden afgeremd door z’n vaccum-verwachtingswaarde, terwijl de zwakke ijkbosonen drie-vierde van de Higgs opgegeten hebben.Ten slotte hebben we aangetoond dat we daadwerkelijk 3/4de van de Higgs uit het Standaard Model al lang ontdekt hebben en dat er een reden is dat de overgebleven Higgs bijzonder is en de Higgs wordt genoemd. Het is de specifieke mate van bewegingsvrijheid dat resulteert in de vacuum-verwachtingswaarde waarmee de ijksymmetrie verbroken wordt (waardoor het opeten van z’n broertjes wordt toegelaten). De Higgs levert nieuwe inzichten in de natuurkunde waardoor de zogenaamde elektrozwakke symmetriebreking plaatsvindt. Als we de Higgs niet gevonden hadden, hadden we een andere wiskundige oplossing moeten bedenken voor de inconsistenties van WW-verstrooiing bij hoge energieën. Zo, dat was het. Ik heb soms misschien dingen iets te letterlijk vertaald – ook zijn er bepaalde fascetten in het verhaal die, ook voor mij, lastig te volgen zijn en nog lastiger zijn uit te leggen. Maar ik ben al lang blij dat ik dit verhaal in begrijpelijk Nederlands heb kunnen brengen. Ik ga m’n zweet afvegen en op m’n gemak een peuk roken 😀 Bron: Quantum Diaries.
Voetnoten







Ok voor de liefhebbers……het is niet het beste platform, maar deze cursus mag je eigenlijk niet missen. Pittige stof maar wel poepieleuk om te doen. De lecture videos zitten goed in elkaar, en Higgs komt regelmatig aan het woord, interview-stijl. Het zit nu in week 4 van 7 weken maar je kan nog instappen. Hier krijg je aan het einde van de cursus geen certificaat o.i.d. maar dat mag geen drempel zijn.
https://www.futurelearn.com/courses/higgs
Ps, email addie is genoeg om je aan te melden…
Sjeezus Olaf, hoe lang ben je met dit stuk bezig geweest? Goed blog!
Ik lees het morgen nog een keer goed door, het is alweer veel te laat 🙂
Olaf, bedankt voor de blog. Taaie materie, die Higgs bosonen, maar verhelderend verhaal.
Nou……bijna aan het einde van de Higgs cursus…..zegt Higgs;
Voor de elektrozwakke symmetriebreking hebben we 16 quantum states
Massless W+, W- en W3 = 3 x 2 = 6 states
Massles B = 1 x 2 = 2 states
2 Higgs fields = 2 x 4 = 8 states
———————————————
16 states
Na de elektrozwakke symmetriebreking hebben we
Massive W+ en W- = 2 x 3 = 6 states
Massive Z = 1 x 3 = 3 states
Massles photon A = 1 x 2 = 2 states
Higgs particles = 5 states
———————————————-
16 states
Met als conclusie, om weer op een totaal van 16 states te komen moeten er dus 5 Higgs zijn, en we hebben er nu 1 gevonden. “We have only scratched the surface when we found the first one”
Ik heb even naar het bron artikel gekeken en daar staan reacties onder van 3 jaar geleden. Misschien is dat artikel inmiddels achterhaald. Of ik snap nog steeds de ballen van quantum theorie, dat kan ook haha
Hou het maar bij het laatste, zou ik ook doen 🙂