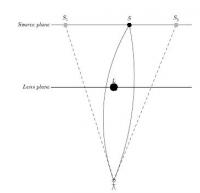
Een zwaartekrachtlens (ook wel gravitatielens genoemd) is een zeer sterk zwaartekrachtveld, bijvoorbeeld van een sterrenstelsel of een zwart gat, dat het licht van een daarachterliggend object afbuigt. Dit lens-effect treedt op, wanneer waarnemer, zwaartekrachtveld (lens) en achterliggende voorwerp (bron) ongeveer op
Wiskundigen lossen zwaartekrachtlens-probleem op
17 juni 2008 door Reageer
Laat wat van je horen