Net als je denkt dat het niet gekker kan, heeft de kwantummechanica ons opnieuw verbaasd. Na de Kat van Schrödinger zijn het nu kwantumduiven die ons op de proef stellen. Kun je namelijk drie duiven kwijt in twee duivenhokken, zonder dat twee duiven in één hok zitten? Nee, toch? Nou ga er even goed voor zitten, want onderzoekers zijn met een persbericht gekomen waarvan je brein vermoedelijk pijn gaat doen.
Als je drie duiven in twee hokken stopt, dan moeten minstens twee duiven in één hok terecht komen – dat is een voor de hand liggende en fundamentele stelling, aangezien het de essentie van het begrip “tellen” omvat. Maar in ons onderzoek hebben we aangetoond dat dit in kwantummechanica niet altijd waar hoeft te zijn! We hebben namelijk een aantal gevallen waargenomen waarbij drie kwantumdeeltjes in twee doosjes zijn gestopt, zonder dat twee deeltjes in hetzelfde doosje zitten. Het is nog te vroeg om te voorspellen wat de implicaties van ons onderzoek zullen zijn. Maar wij zijn persoonlijk van mening dat de implicaties enorm zullen zijn, aangezien we te maken hebben met hele fundamentele concepten.
Wauw. De natuurkunde-fanaten kunnen het hele onderzoek hier bekijken.
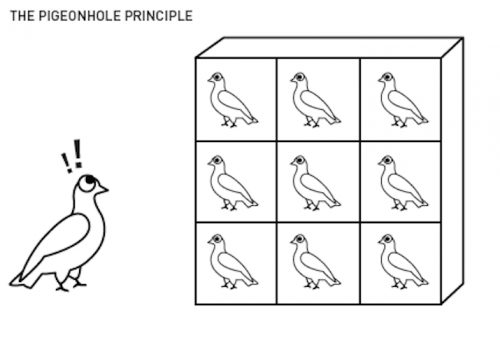





Waar ik echt benieuwd naar ben is 2 vragen: wat is een “kwantumdeeltje?” en “hoe stop je een kwantumdeeltje in een doosje?”. Ik ben nog van de generatie die grote twijfels heeft aan kwantummechanica, en zover ik begrijp gaat het om super kleine deeltjes, die je nauwelijks of niet kan zien, laat staan aanraken en ergens instoppen. Of nog specifieker: zo klein dat je ze niet van elkaar kan onderscheiden. Dus 1 deeltje in 1 doosje stoppen, dat klinkt eenvoudig, maar is volgens mij al onhaalbaar. Maar ik lees graag meer.
Niet zo heel spooky…het zijn de elementaire deeltjes https://nl.wikipedia.org/wiki/Standaardmodel_van_de_deeltjesfysica
En waar ik benieuwd naar ben: wat gebeurt er met die drie duiven als Schrödingers kat ze in de smiezen krijgt? 😉
groet,
Gert (momenteel alleen thuis, dus inderdaad de leukste)
😛 Daar heeft Schrödingers kat een hele kluif aan, 3 duiven. Maar over die duivenhokken…
Je maakt van twee duivenhokken 3 compartimenten door ze gedeeltelijk in elkaar te schuiven. Het middelste gedeelte (â…“) is voor duif 3 Probleem opgelost.
Nee?
Zou best kunnen Monique. Ik heb me er nog niet in verdiept. Ben momenteel bezig met een boek over non-localiteit. Daar heb ik een hele kluif aan.
mvg,
Gert
die kat zal het een worst wezen hoeveel duiven in een hok zitten, die heeft 3 dagen aan eten in huis.
Die kat is de helft van de tijd dood, dus hij kan er zelfs zes dagen mee doen. 😉
groet,
Gert (Enceladus)
Hier wat andere en iets minder technische artikelen 🙂 :
http://www.sciencedaily.com/releases/2016/01/160120112110.htm
http://phys.org/news/2016-01-pigeons-pigeonholes-hole.html
http://www.dailymail.co.uk/sciencetech/article-3409392/Forget-Schrodingers-cat-researchers-reveal-quantum-pigeonhole-principle-say-tests-basic-notion-physics.html
Elementaire deeltjes bestaan niet echt in de zin waarin een object in de macrosfeer bestaat. Aannemelijk is dat buiten het geval van waarneming en het instorten van de waarschijnlijkheidsgolf een deeltje niet bestaat op een bepaalde plaats met een bepaalde richting, maar verspreid is over de ruimte waarin het naar de wetten van de waarschijnlijkheid bij waarneming kan opduiken. Om in de beeldspraak te blijven: de drie duiven zijn verspreid over een grote ruimte waarbinnen zich ook de twee hokken bevinden.
Volgens mij kun je het beste uitgaan van de gedachte dat alles bestaat uit golven. Je hebt daar verschillende typen in die verschillend op elkaar reageren. Materie kun je dan zien als gelocaliseerde golven, beschreven met golf-functies, die b.v. een bepaalde interactie hebben met zwaartekracht (-golven), waardoor zich dat vertaalt in een “massa”.
Bundelingen van dergelijke gelocaliseerde materiegolven hebben een bepaalde interactie met elkaar; daardoor gedragen ze zich gezamenlijk als een deeltje of een biljartbal of een andere fysisch-mechanische vorm, die we waarnemen in de macro-wereld.
Niels, bedankt voor je reactie. De blog was niet helemaal compleet meer, maar dat heb ik zojuist weer hersteld. Lees wat gemakkelijker. 🙂