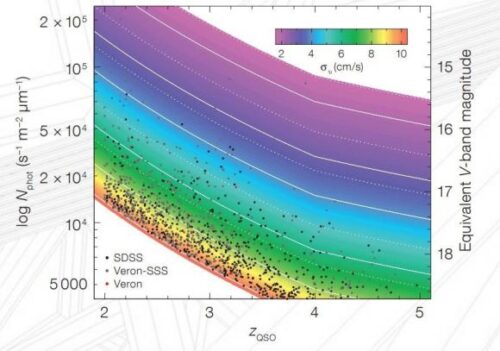
De theoretische roodverschuivingsdrift gebaseerd op het standaard-heelalmodel. Credit: ESO / ELT Science Case
Hebben we het over de snelheid waarmee het heelal uitdijt dan hebben we het negen van de tien keer over de Hubble constante, de constante die de verhouding weergeeft van de snelheid waarmee een bepaalde afstand van een sterrenstelsel groter wordt door de uitdijing van het heelal en de grootte van die afstand, uitgedrukt in km per seconde per megaparsec. Er is veel gedoe over de waarde van H0 (yep, de Hubble spanning), maar grosso modo is H0 rond de 70 km/s/Mpc, wat wil zeggen dat een sterrenstelsel op 1 megaparsec afstand (=3.260.000 lichtjaar) met 70 km/’s van ons af beweegt en een stelsel op 2 Mpc afstand met 140 km/s, enzovoorts. Afstand wordt door sterrenkundigen uitgedrukt in lichtjaar, maar het kan ook in roodverschuiving z, hetgeen ik onder andere hier heb uitgelegd. En daarover is door een groepje sterrenkundigen onlangs een nieuw voorstel voor bedacht om de uitdijingssnelheid van het heelal mee te meten: met behulp van de zogeheten roodverschuivingsdrift (Engels: redshift drift). Het idee erachter is eigenlijk heel simpel: een sterrenstelsel op verre afstand van de aarde heeft een bepaalde roodverschuiving c.q. afstand (het komt op hetzelfde neer), bijvoorbeeld het stelsel GHZ2/GLASS-z12 dat volgens de metingen met Webb een roodverschuiving van z∼12,2 heeft, d.w.z dat het nu 32 miljard lichtjaar van ons vandaan staat. Maar ja, de roodverschuiving van GHZ2/GLASS-z12 is geen constante, het is nù op dit moment as we speak z∼12,2. Maar hoeveel is het over een jaar, dan is het stelsel verder van de aarde geraakt en dan is het wellicht z∼12,200000000000001. En da’s precies wat ze met de roodverschuivingsdrift bedoelen: de verandering van de roodverschuiving (of afstand) als gevolg van de uitdijing van het heelal.
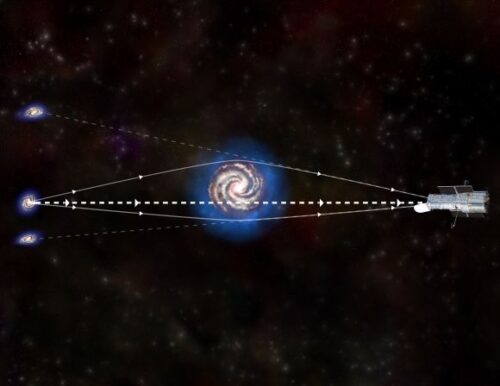
Maar ja, GHZ2/GLASS-z12 (op de foto hierboven in beeld) staat hééél ver weg en om na een jaar te meten hoeveel de roodverschuiving gegroeid is lijkt onbegonnen werk. Voor een stelsel op zo’n afstand bedraagt die drift naar schatting zo’n 15 cm/s per jaar (zie afbeelding bovenaan), dus hoe meet je dat in hemelsnaam? Op dit moment lijkt het meten van die drift inderdaad een stap te ver, zelfs met Webb gaat dat niet lukken. Maar Chengyi Wang en zijn collega’s denken dat het met de Europese Extremely Large Telescope (ELT), die naar verwachting in 2027 in gebruik wordt genomen, wél gaat lukken. Daarmee zou het mogelijk moeten zijn om in theorie roodverschuivingsdriften van slechts 5 cm/s te meten. Hoe ze dat doen? Door gebruik te maken van die megatelescoop én van zwaartekrachtlenzen van sterrenstelsels. Zoals onderstaande afbeelding laat zien kan het licht van ver verwijderde sterrenstelsels onderweg naar de aarde verschillende paden bewandelen om ons te bereiken en die paden zijn niet allemaal even lang… ergo: het licht van een achtergrondstelsel kan op verschillende momenten bij de aarde arriveren.
En da’s de kern van het voorstel: in plaats van decennia te wachten om een minimini-verschuiving in de roodverschuiving te meten kan je een stelsel waarnemen dat door een zwaartekrachtlens in meerdere beelden is gesplitst, met verschillende aankomsttijden van het licht bij de aarde, en door die aankomsttijden exact te meten met voldoende grote telescopen á la ELT kan je de drift meten. En zo heb je een exact beeld van de snelheid waarmee het heelal uitdijt.
En da’s allemaal na te lezen in het artikel van Wang, Chengyi, Krzysztof Bolejko, and Geraint F. Lewis. “The Redshift Difference in Gravitational Lensed Systems: A Novel Probe of Cosmology.” arXiv preprint arXiv:2308.07529 (2023).
Bron: Universe Today.



Het verschil met H0LiCOW (Wong et al) en dit ELTvoorstel (Wang et al) is dat Wong een tijd referentie gebruikt in de vorm van een betrouwbare event zoals een flare o.i.d. en Wang (zoal ik het lees) alleen het verschil in roodverschuiving bestudeerd, dus zonder een event (dat lukt ook vast niet met de beoogde gelensde 1000 stelsels). Je zou m.i. ook de absolute onderlinge posities van de projecties kunnen gebruiken die “snel” uit focus raken op deze grote afstand door zowel de expansie zelf en dus verschuiving van het lensbrandpunt t.o.v. het object en de enorme versterkingsfactor.