Dát het heelal uitdijt weten we al sinds 1927, toen Edwin Hubble het idee van het uitdijende heelal van George Lemaître dankzij de roodverschuiving van sterrenstelsels kon bevestigen, en dat het heelal versneld uitdijt weten we sinds 1998, door twee onafhankelijke teams van sterrenkundigen gemeten … [Lees meer...]
Nee, de Cepheïden kunnen de Hubble spanning niet helpen oplossen
De Hubble spanning is tezamen met de S8-spanning één van de grootste problemen waar de hedendaagse kosmologie tegenaan loopt. Sterrenkundigen weten sinds eind jaren twintig van de vorige eeuw dat het heelal uitdijt, sinds 1998 dat het heelal versnelt uitdijt, maar niet hoe snel het heelal uitdijt. … [Lees meer...]
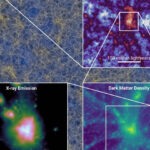
FLAMINGO: donkere materie, gewone materie en neutrino’s in grootste kosmologische simulatie ooit
Een internationaal team van astronomen heeft de grootste kosmologische computersimulatie ooit uitgevoerd, die niet alleen donkere maar ook gewone materie volgt. De FLAMINGO-simulatie berekent de evolutie van alle componenten van het heelal - gewone materie, donkere materie en donkere energie - … [Lees meer...]
Nieuwe manier om uitdijingssnelheid heelal te meten: m.b.v. de roodverschuivingsdrift
Hebben we het over de snelheid waarmee het heelal uitdijt dan hebben we het negen van de tien keer over de Hubble constante, de constante die de verhouding weergeeft van de snelheid waarmee een bepaalde afstand van een sterrenstelsel groter wordt door de uitdijing van het heelal en de grootte van … [Lees meer...]
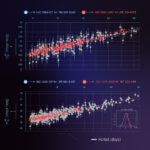
Webb’s metingen aan Cepheïden houden de Hubble spanning in stand
Sinds pak 'm beet 2016 is er een discussie tussen sterrenkundigen over de snelheid waarmee het heelal uitdijt en die tussen twee 'kampen' gevoerd wordt, een kamp van het vroege heelal die een uitdijingssnelheid H0 van 67 á 68 km/s/Mpc heeft gemeten en een kamp van het lokale, huidige heelal, die op … [Lees meer...]
Mogelijk is het heelal helemaal niet ‘antropisch’, afgestemd op de de mens
Jullie kennen 'm vast wel, het antropische principe, het principe dat er in meerdere varianten is en dat er op neer komt dat er een nauw verband bestaat tussen ons mens-zijn en de eigenschappen van het heelal. Verander je iets aan de natuurconstanten, bijvoorbeeld de fijnstructuur-constante of de … [Lees meer...]
Babyheelallen van een multiversum als primordiale zwarte gaten?
Het was een bizar jaar, dus laten we 'm maar gelijk afsluiten met een bizarre theorie, zoals ik 'm toch wel wil kenmerken. Een internationaal team van sterrenkundigen, waaronder Alexander Kusenko, Misao Sasaki, Sunao Sugiyama, Masahiro Takada en Volodymyr Takhistov (Kavli Institute for the Physics … [Lees meer...]
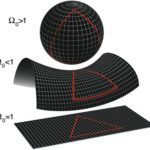
Is de ruimte in het heelal nou vlak of toch gekromd?
Toen in 2018 de definitieve gegevens van de Europese Planck missie werden gepubliceerd, de ruimteverkenner die de kosmische microgolf-achtergrondstraling had bestudeerd (Engels: CMB), waren de meeste sterrenkundigen ervan overtuigd dat de ruimte in het heelal vlak is (Engels: flat). Dat betekende … [Lees meer...]
Nee, het heelal als geheel roteert niet
Alle hemelobjecten draaien om hun as, sterren zoals de zon, planeten zoals de aarde, kometen, planetoïden, noem het maar op. Logische veronderstelling dat het grootste wat er is ook misschien wel roteert, het heelal zelf. Nou is het natuurlijk de vraag hoe je dat zou moeten waarnemen, want het … [Lees meer...]
(555) – 711 – 2555, het telefoonnummer van het heelal
Ik kwam vanochtend deze tweet tegen, waarin een afbeelding wordt getoond die de schaal van het heelal laat zien, van het allerkleinste (een atoomkern) tot het allergrootste (het heelal zelf). In stapjes van machten van tien zie je hoe je van het kleinste tot het grootste komt. En laten de tien … [Lees meer...]